Secure Multi-Party Computation

An in-depth exploration of Secure Multi-Party Computation (SMPC) and its practical implementation in data privacy.

Secure Multi-Party Computation (SMPC) is crucial for maintaining data confidentiality while enabling secure computations, positioning SMPC as a key technology for privacy-preserving solutions.

As organizations increasingly handle sensitive data—from financial transactions to healthcare records—the urgency for secure data collaboration mechanisms has escalated. SMPC is particularly pertinent in various sectors, such as:

✔ Finance – Enabling secure analysis of transaction data while preserving individual account confidentiality.

✔ Healthcare – Allowing collaborative medical research without compromising patient privacy. 

✔ Data Analytics – Extracting insights from encrypted datasets without exposing the underlying raw data

This article explores both the theoretical and practical aspects of SMPC, encompassing fundamental cryptographic principles that frame SMPC and common protocols such as secret sharing and garbled circuits.

What is Secure Multi-Party Computation?

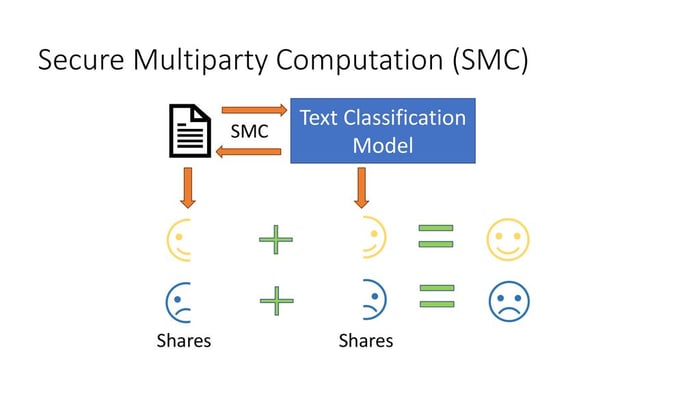
Secure Multi-Party Computation (SMPC) is a cryptographic technique that enables multiple parties to jointly compute a function over their private inputs while ensuring that:

✔ Data Privacy – Each party’s input remains confidential and is never disclosed to others.
✔ Correctness – The computation produces accurate results without requiring trust in any single participant.
✔ No Single Point of Trust – No individual entity gains control over the full dataset or computation process.

SMPC ensures that even if some participants act maliciously, they cannot access or alter the private data of others, making it a cornerstone of privacy-preserving cryptography.

History & Cryptographic Foundations

The concept of SMPC emerged from cryptographic research in the 1980s, with foundational work including:

• Yao’s Garbled Circuits (1982) – Andrew Yao introduced a method for securely evaluating Boolean circuits, laying the groundwork for SMPC.

• Secret Sharing (Shamir, 1979) – A technique for distributing a secret among multiple parties, enabling fault-tolerant SMPC.

• GMW Protocol (1987) – Goldreich, Micali, and Wigderson extended Yao’s work to multi-party computations.

Over the years, advancements in homomorphic encryption, zero-knowledge proofs, and differential privacy have further strengthened SMPC’s security and efficiency.

Key Concepts and Protocols in SMPC

SMPC allows multiple parties to jointly compute a function on their private data without revealing their inputs. Below are the core building blocks and key protocols used in SMPC.

Core Building Blocks

SMPC relies on cryptographic techniques to ensure privacy and correctness. The main techniques include:

1. Secret Sharing

Secret sharing splits a private value into multiple pieces (shares) distributed among participants. No single participant can reconstruct the original value alone.

• Shamir’s Secret Sharing (SSS): Uses polynomial interpolation to ensure that only a minimum number of participants (threshold tt) can reconstruct the secret.

• Additive Secret Sharing: Splits a secret into random shares, where the sum of all shares equals the secret. Used in modern SMPC frameworks like SPDZ.

2. Oblivious Transfer (OT)

A method where:

• A sender has two secret values.

• A receiver picks one without revealing their choice to the sender.

• The sender does not know which value was chosen.

Use Case: Enables secure function evaluation without leaking unnecessary information.

3. Homomorphic Encryption (HE)

Allows computations on encrypted data without decrypting it.

• Partially Homomorphic Encryption (PHE): Supports only addition or multiplication (e.g., RSA, ElGamal).

• Fully Homomorphic Encryption (FHE): Supports both but is computationally expensive (e.g., Gentry’s scheme).

Use Case: Privacy-preserving machine learning and secure cloud computations.

4. Yao’s Garbled Circuits

A two-party computation method where a function is converted into an encrypted Boolean circuit. The circuit can be evaluated without revealing intermediate values.

Use Case: Secure auctions, private set intersection, and secure machine learning.

Popular SMPC Protocols

Different protocols optimize for efficiency, scalability, and security based on the application.

Choosing the Right Protocol

• For Boolean operations → GMW / Yao’s Garbled Circuits

• For arithmetic computations → SPDZ

• For hybrid computations → ABY

Each protocol has trade-offs in efficiency, scalability, and security. The right choice depends on the application and the level of security required.

Implementing SMPC in Practice

Implementing SMPC requires specialized tools, careful environment setup, and performance optimizations to make computations efficient and scalable.

Several libraries and frameworks provide ready-to-use SMPC implementations, reducing the complexity of cryptographic operations.

Building a Simple SMPC Application

Let’s implement secure addition using PySyft and MP-SPDZ.

Step 1: Install PySyft

pip install syft

Step 2: Initialize Virtual Workers

import syft as sy


# Create virtual workers (simulating separate parties)
alice = sy.VirtualWorker(hook, id="alice")
bob = sy.VirtualWorker(hook, id="bob")

Step 3: Secret Share a Number

x = 42  
shared_x = x.share(alice, bob)  # Secret share the number between Alice and Bob

Step 4: Perform Computation on Encrypted Data

y = 58  
shared_y = y.share(alice, bob)  


result = shared_x + shared_y  
print(result.get())  # Output: 100 (computed securely)

The computation happens without revealing the inputs to any single party!

Challenges and Optimization

While SMPC provides strong security guarantees, it also faces performance bottlenecks that must be addressed for real-world applications.

Optimization Techniques

• Protocol Selection: choosing the appropriate cryptographic protocol is crucial for optimizing performance and security based on the type of operations being executed.

  • GMW/Yao Protocols for Boolean Operations: The GMW protocol is advantageous for multiple parties and numerous Boolean gates, utilizing a hybrid of symmetric and asymmetric encryption. In contrast, Yao’s protocol excels with fewer parties, offering strong security but often has higher computational costs during garbling.

  • SPDZ for Arithmetic Operations: This protocol utilizes secret sharing and homomorphic encryption for efficient computation over shared secrets while preserving operand privacy. SPDZ is ideal for applications demanding efficiency and low latency in large-scale arithmetic computations, balancing privacy and performance.

• Preprocessing: The preprocessing phase is critical for enhancing the efficiency of the online phase in SMPC.

  • Precompute Randomness (e.g., Beaver’s Triples): Using Beaver's triples allows for the precomputation of random values, reducing expensive computations during the online phase. These triplets (a, b, c) satisfy c = a * b and are shared among parties, enabling multiplication without direct interaction, thus significantly reducing overall execution time.

• Parallelization: 

  • Running Computations in Parallel: To minimize execution time, leverage parallel processing by distributing tasks across multiple processors or nodes. This improves throughput and reduces processing time for large-scale computations, especially when many independent operations can be computed simultaneously.

• Hybrid SMPC + Homomorphic Encryption (HE): 

  • Use of HE for Lightweight Operations: In mixed workload applications, using homomorphic encryption (HE) for lightweight operations can be advantageous, as it enables computations on ciphertexts while maintaining data privacy. This is particularly useful for simple aggregations or queries without the overhead of secure multi-party computation (SMPC).

  • Switch to SMPC for Heavy Computation: For complex operations requiring substantial computational resources, adopting an SMPC-based approach is recommended. This strategy allows less intensive tasks to benefit from HE's efficiency, while heavier tasks gain from SMPC's security, striking a balance between performance and privacy.

This structured approach to combining different cryptographic protocols and computational strategies can significantly enhance the efficiency and effectiveness of secure data processing tasks in various applications.

SMPC Industry Use Cases

Secure Multi-Party Computation (SMPC) has transitioned from theoretical cryptography to real-world applications across industries requiring secure collaboration on sensitive data. This section explores how SMPC is applied in finance, healthcare, and advertising, along with real-world challenges and solutions.

Finance: Fraud Detection & Risk Analysis

Financial institutions need to detect fraudulent transactions and assess risk across multiple banks without exposing sensitive customer data to competitors.

SMPC Solution

• Multiple banks jointly compute fraud risk scores without sharing individual customer data.

• SMPC allows collaborative analysis of suspicious transactions while preserving privacy.

• Example: A consortium of banks uses SMPC to identify fraudulent activities across institutions without disclosing private account details.

Challenges & Solutions

Healthcare: Secure Genomic Research & Disease Prediction

Medical researchers need access to diverse patient genomic data for disease prediction and drug development, but privacy laws (e.g., HIPAA, GDPR) restrict direct data sharing.

SMPC Solution

• Hospitals & research institutions collaborate on genomic data analysis using SMPC.

• Enables multi-party genome-wide association studies (GWAS) without exposing patient data.

• Example: Researchers apply SMPC to analyze Alzheimer’s disease genetic risk across hospitals in different countries.

Challenges & Solutions

Advertising: Private Matching & Attribution Analysis

Advertisers and social media platforms need to match customer data for targeted advertising without compromising user privacy.

SMPC Solution

• Companies can jointly compute overlapping customer segments without revealing individual user data.

• Example: Facebook & Google use SMPC to perform privacy-preserving ad conversions while ensuring compliance with privacy regulations like GDPR & CCPA.

Challenges & Solutions

Conclusion

SMPC plays a vital role in enabling secure, privacy-preserving computations across various industries. By leveraging cryptographic techniques such as secret sharing, oblivious transfer, homomorphic encryption, and garbled circuits, SMPC ensures that sensitive data remains protected while allowing meaningful analysis and collaboration.

The growing need for privacy-enhancing technologies is driving the rapid adoption of SMPC in finance, healthcare, and data analytics. As regulatory frameworks increasingly emphasize data protection, businesses and researchers must integrate SMPC solutions to comply with privacy laws while maintaining analytical capabilities. Despite computational challenges, advancements in cryptographic techniques and hardware acceleration are improving the efficiency of SMPC, making it more practical for real-world applications.

Moving forward, continued research and innovation in SMPC will be essential for addressing scalability concerns and optimizing performance. As industries adopt privacy-preserving technologies, SMPC will serve as a cornerstone for secure and ethical data collaboration in the digital age.

Akava would love to help your organization adapt, evolve and innovate your modernization initiatives. If you’re looking to discuss, strategize or implement any of these processes, reach out to bd@akava.io and reference this post.